O Que É Sequência De Fibonacci Exemplos – Com a Sequência de Fibonacci: Definição, Geração e Aplicações em destaque, este parágrafo abre uma janela para um início surpreendente e intrigante, convidando os leitores a embarcar em uma jornada de descobertas e insights inesperados.
A Sequência de Fibonacci é uma sequência numérica fascinante com propriedades matemáticas únicas e aplicações práticas em vários campos. Vamos mergulhar em seu conceito, fórmula, propriedades e usos para entender sua importância e beleza.
Sequência de Fibonacci: O Que É Sequência De Fibonacci Exemplos
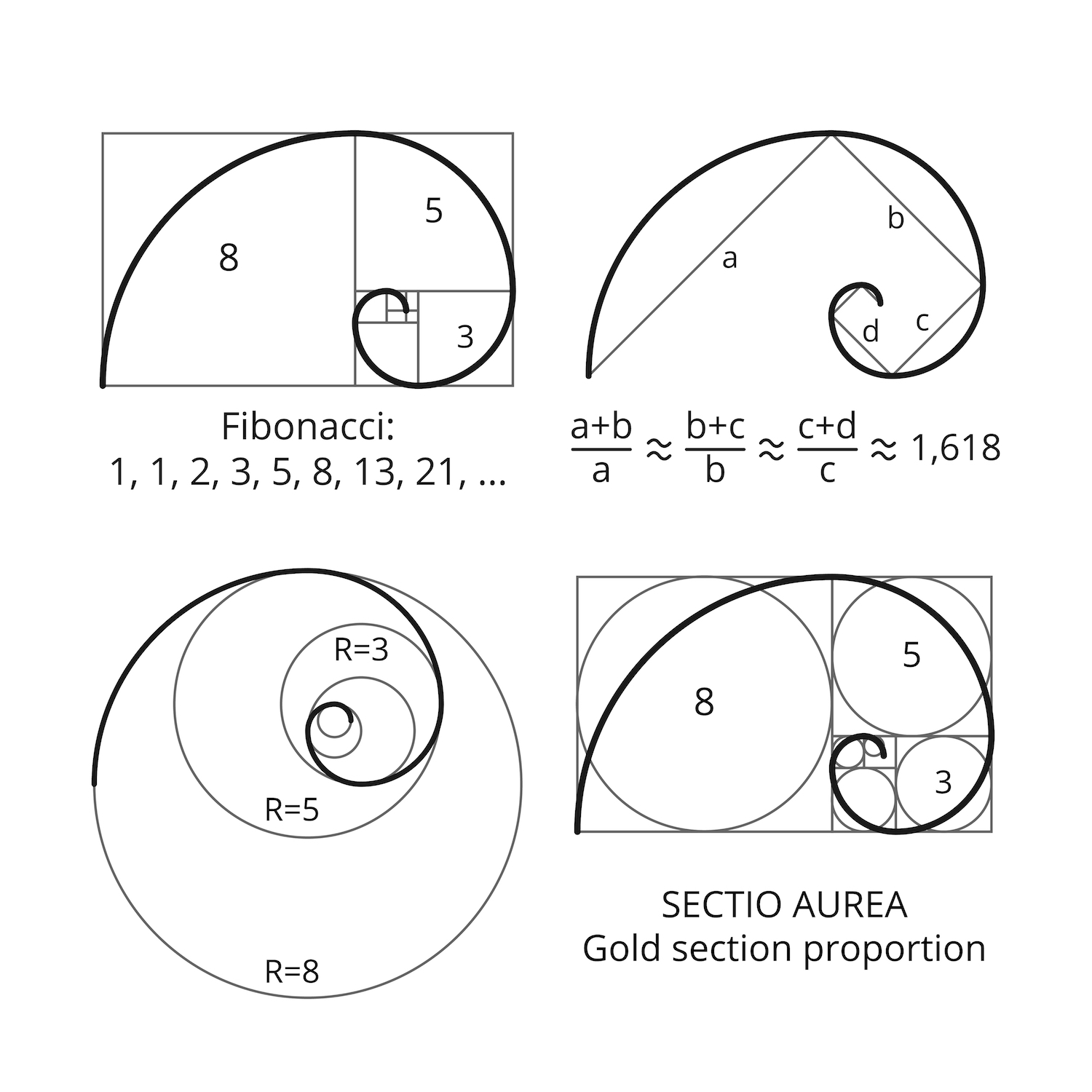
A Sequência de Fibonacci é uma sequência numérica infinita onde cada número é a soma dos dois números anteriores. A sequência começa com 0 e 1, e continua assim: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …A
fórmula para encontrar o próximo número na sequência é:“`F(n) = F(n-1) + F(n-2)“`Onde F(n) é o n-ésimo número da sequência.
Fórmula e Geração da Sequência
A sequência de Fibonacci é uma sequência de números onde cada número é a soma dos dois números anteriores. A sequência começa com 0 e 1, e os próximos números são gerados somando os dois números anteriores.
Fórmula
A fórmula para gerar a sequência de Fibonacci é:“`F(n) = F(n-1) + F(n-2)“`Onde:* F(n) é o n-ésimo termo da sequência
- F(n-1) é o (n-1)-ésimo termo da sequência
- F(n-2) é o (n-2)-ésimo termo da sequência
Geraçãodos Números
Os primeiros números da sequência de Fibonacci são:“`
, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
“`Para gerar os números da sequência, basta aplicar a fórmula para cada número. Por exemplo, para gerar o 5º número da sequência, basta somar o 4º e o 3º números:“`F(5) = F(4) + F(3)F(5) = 3 + 2F(5) = 5“`Portanto, o 5º número da sequência de Fibonacci é 5.
Aplicações Práticas da Sequência

A sequência de Fibonacci encontra aplicações práticas em vários campos, desde a natureza até a ciência e a arte. Sua presença pode ser observada em padrões de crescimento, arranjos musicais e até mesmo em algoritmos de programação.
Na Natureza, O Que É Sequência De Fibonacci Exemplos
Na natureza, a sequência de Fibonacci aparece em padrões de crescimento de plantas, conchas e até mesmo galáxias. Por exemplo, o número de pétalas em uma flor pode seguir a sequência, assim como o arranjo das folhas em um caule.
Na Arte
Na arte, a sequência de Fibonacci é usada para criar harmonia e equilíbrio em composições. Por exemplo, os pintores renascentistas usavam a proporção áurea, derivada da sequência, para criar composições visualmente agradáveis.
Na Ciência
Na ciência, a sequência de Fibonacci é usada em algoritmos de busca e otimização. Por exemplo, o algoritmo de Fibonacci é usado para encontrar o menor caminho entre dois pontos em um grafo.
Tabela de Aplicações
| Campo | Aplicação |
|---|---|
| Natureza | Padrões de crescimento, arranjos de folhas |
| Arte | Proporção áurea, composição visual |
| Ciência | Algoritmos de busca e otimização |
Extensões e Variações da Sequência

A sequência de Fibonacci possui diversas variações e extensões que ampliam sua aplicabilidade em diferentes áreas. Essas variações mantêm a relação fundamental da sequência original, mas introduzem novos elementos ou modificações.
Sequência de Fibonacci Generalizada
A sequência de Fibonacci generalizada é uma extensão que permite a definição de uma sequência com dois números iniciais quaisquer e uma constante de razão. A fórmula geral para essa sequência é:
F(n) = a + b – (φ^n – ψ^n) / (φ – ψ)
Onde:
- a e b são os números iniciais
- φ e ψ são as raízes da equação x^2 – x – 1 = 0
- n é o índice do termo
Espiral Áurea
A espiral áurea é uma espiral logarítmica baseada na proporção áurea, que é aproximadamente 1,618. É formada pela sucessão de quadrados cujo lado é igual ao próximo número da sequência de Fibonacci. A espiral áurea é encontrada em vários fenômenos naturais e obras de arte, sendo considerada uma forma esteticamente agradável.
Comparação de Variações
| Variação | Fórmula | Aplicação |
|---|---|---|
| Sequência de Fibonacci | F(n) = F(n-1) + F(n-2) | Modelagem de crescimento, finanças |
| Sequência de Fibonacci Generalizada | F(n) = a + b
|
Modelagem de fenômenos não lineares |
| Espiral Áurea | – | Estética, design, arquitetura |
A Sequência de Fibonacci é uma ferramenta valiosa que oferece insights em diversos campos, desde a natureza até a arte e a ciência. Suas propriedades matemáticas e aplicações práticas continuam a inspirar e fascinar, tornando-a um tema inesgotável de exploração e descoberta.
Questions Often Asked
O que é a Sequência de Fibonacci?
É uma sequência numérica em que cada número é a soma dos dois números anteriores. A sequência começa com 0 e 1, e continua assim: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34…
Como a Sequência de Fibonacci é gerada?
Cada número da sequência é a soma dos dois números anteriores. Portanto, a fórmula para gerar a sequência é F(n) = F(n-1) + F(n-2), onde F(n) é o n-ésimo número da sequência.
Quais são algumas das propriedades da Sequência de Fibonacci?
A sequência tem várias propriedades matemáticas interessantes, como a Proporção Áurea (1,618), que é a razão entre dois números consecutivos da sequência à medida que ela se aproxima do infinito.
Quais são as aplicações práticas da Sequência de Fibonacci?
A sequência é usada em vários campos, incluindo design, música, ciência e finanças. Por exemplo, a Proporção Áurea é frequentemente usada em design e arquitetura para criar composições esteticamente agradáveis.

