Exercícios Sobre Equação Do 2º Grau (Com Questões Resolvidas E) apresenta uma análise completa e detalhada da resolução de equações quadráticas. Abordaremos os diferentes tipos de equações – completas, incompletas puras e incompletas mistas – explicando seus métodos de resolução, incluindo a fórmula de Bhaskara e a fatoração. Além disso, exploraremos aplicações práticas em diversas áreas, como geometria e física, ilustrando a utilidade dessas equações na modelagem de fenômenos reais.
A interpretação dos resultados, incluindo a análise do discriminante e o significado de raízes reais e complexas, também será discutida, garantindo uma compreensão abrangente do tema.
O estudo das equações do segundo grau é fundamental para a compreensão de conceitos matemáticos mais avançados e para a resolução de problemas em diversas áreas do conhecimento. Este material visa fornecer aos estudantes uma base sólida, através de exercícios resolvidos e exemplos práticos, facilitando a assimilação dos conceitos e desenvolvendo a capacidade de aplicar o conhecimento adquirido na solução de problemas.
Tipos de Equações do 2º Grau e suas Resoluções: Exercícios Sobre Equação Do 2º Grau (Com Questões Resolvidas E
As equações do segundo grau são expressões algébricas da forma ax² + bx + c = 0, onde a, b e c são constantes reais e a ≠ 0. A compreensão de seus diferentes tipos e métodos de resolução é fundamental para diversas aplicações em matemática e áreas afins. Esta seção detalha os tipos de equações do segundo grau e os métodos utilizados para encontrar suas raízes (ou soluções).
Classificação das Equações do 2º Grau
As equações do segundo grau são classificadas em três tipos principais, dependendo dos valores dos coeficientes a, b e c: completa, incompleta pura e incompleta mista. A escolha do método de resolução mais eficiente depende diretamente dessa classificação.
Métodos de Resolução
A resolução de uma equação do segundo grau visa encontrar os valores de x que satisfazem a equação. Os métodos mais comuns são a fórmula de Bhaskara, a fatoração e, para equações incompletas puras, o método da raiz quadrada.
Tabela de Exemplos de Equações do 2º Grau
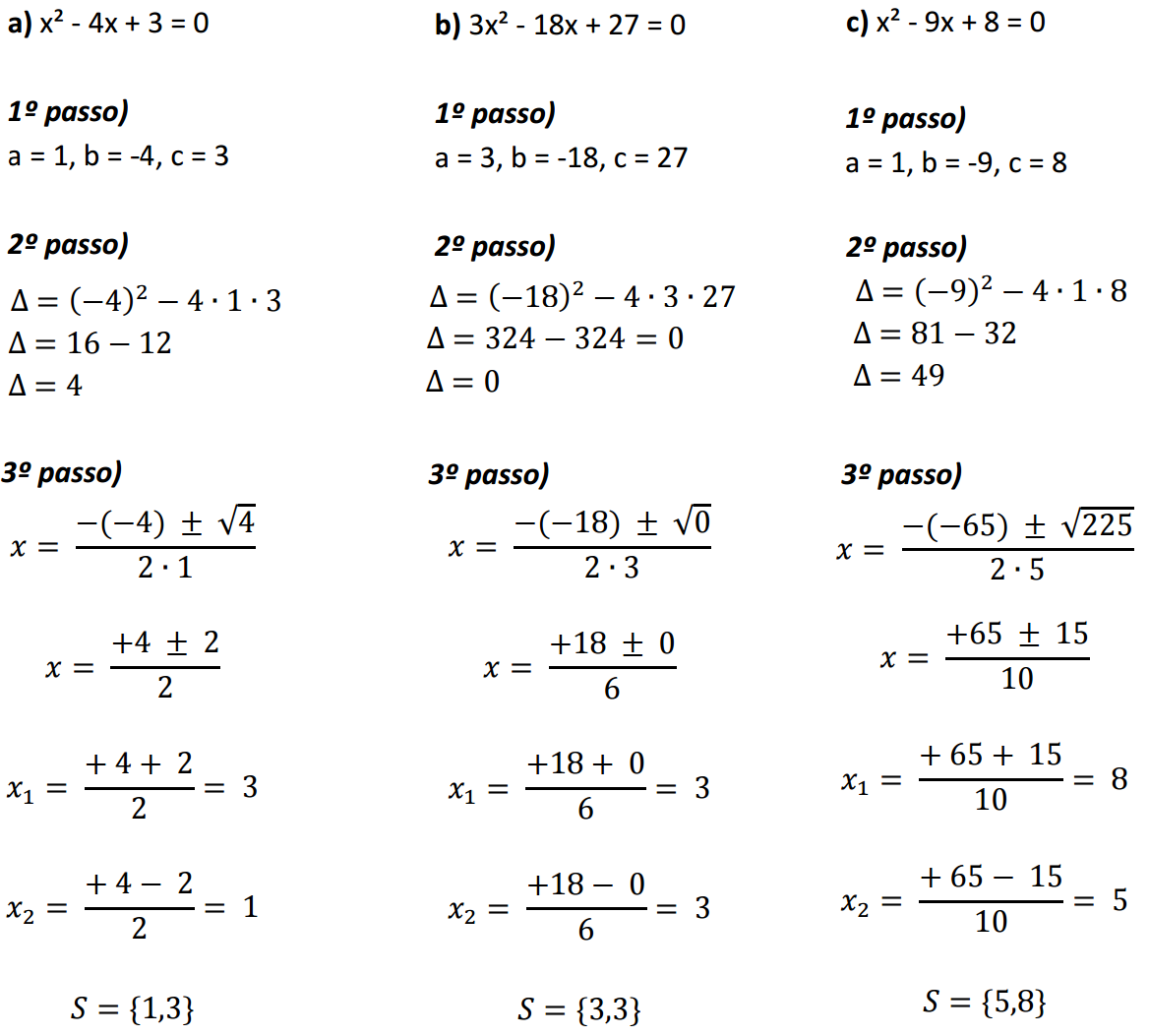
A tabela abaixo ilustra exemplos de cada tipo de equação do segundo grau, o método de resolução mais adequado e suas respectivas soluções.
| Equação | Tipo | Método de Resolução | Solução |
|---|---|---|---|
| x² – 5x + 6 = 0 | Completa | Fatoração ou Fórmula de Bhaskara | x = 2 ou x = 3 |
| x² – 9 = 0 | Incompleta Pura | Método da raiz quadrada | x = 3 ou x = -3 |
| 2x² – 6x = 0 | Incompleta Mista | Fatoração | x = 0 ou x = 3 |
Comparação entre a Fórmula de Bhaskara e a Fatoração

A fórmula de Bhaskara, dada por
x = (-b ± √(b²4ac)) / 2a
, é um método geral aplicável a todas as equações do segundo grau, completas ou incompletas. A fatoração, por sua vez, consiste em encontrar dois binômios cujo produto resulta na equação original. A fatoração é mais rápida quando aplicável, mas nem sempre é possível encontrar fatores inteiros para todas as equações.Exemplo utilizando a fórmula de Bhaskara: Para a equação x²5x + 6 = 0, temos a = 1, b = -5 e c = 6.
Substituindo na fórmula, encontramos x = 2 e x = 3.Exemplo utilizando a fatoração: A equação x²
5x + 6 = 0 pode ser fatorada como (x – 2)(x – 3) = 0, resultando nas mesmas soluções x = 2 e x = 3.
Resolução de Equação do 2º Grau Incompleta Pura pelo Método da Raiz Quadrada
O método da raiz quadrada é aplicado a equações do tipo ax² + c = 0. A resolução envolve isolar o termo com x², calcular a raiz quadrada de ambos os lados da equação e considerar ambos os sinais (positivo e negativo) da raiz.Exemplo: Resolvendo a equação x²
9 = 0
1. Isolar o termo com x²
x² = 9
2. Calcular a raiz quadrada
√x² = ±√9
3. Simplificar
x = ±3Portanto, as soluções são x = 3 e x = -3.
Interpretação de Resultados e Análise de Soluções
A resolução de uma equação do 2º grau, da forma ax² + bx + c = 0 (com a ≠ 0), leva a diferentes tipos de soluções, dependendo dos valores dos coeficientes a, b e c. A interpretação correta dessas soluções é crucial para a compreensão do problema em questão. A análise se baseia no estudo do discriminante e na verificação das raízes encontradas.
Condições para o Número de Raízes Reais

O discriminante, representado por Δ (delta), é dado pela expressão
Δ = b²
4ac
. O valor de Δ determina a natureza das raízes da equação
- Se Δ > 0, a equação possui duas raízes reais e distintas. Isso significa que existem dois valores diferentes de x que satisfazem a equação.
- Se Δ = 0, a equação possui duas raízes reais e iguais (uma raiz real dupla). Neste caso, a equação possui apenas uma solução real.
- Se Δ < 0, a equação não possui raízes reais. As raízes são números complexos, da forma a ± bi, onde 'a' e 'b' são números reais e 'i' é a unidade imaginária (i² = -1).
Verificação de Soluções
Para verificar se uma solução obtida é correta, basta substituí-la na equação original. Se a igualdade for verdadeira, a solução está correta.Exemplo 1: Considere a equação x²5x + 6 = 0. As soluções são x₁ = 2 e x₂ = 3.Verificação para x₁ = 2: (2)²5(2) + 6 = 4 – 10 + 6 = 0. A igualdade é verdadeira, logo x₁ = 2 é uma solução correta.Verificação para x₂ = 3: (3)²5(3) + 6 = 9 – 15 + 6 = 0.
A igualdade é verdadeira, logo x₂ = 3 é uma solução correta.Exemplo 2: Considere a equação x² + 2x + 1 = 0. A solução é x = -1.Verificação para x = -1: (-1)² + 2(-1) + 1 = 1 – 2 + 1 = 0. A igualdade é verdadeira, logo x = -1 é uma solução correta.
Implicações de Raízes Complexas, Exercícios Sobre Equação Do 2º Grau (Com Questões Resolvidas E
Quando o discriminante é negativo (Δ < 0), a equação do 2º grau não possui raízes reais. As soluções são pares de números complexos conjugados. Em contextos físicos ou geométricos, essas raízes podem indicar a inexistência de soluções reais para o problema modelado pela equação. Por exemplo, em um problema que busca as dimensões de um retângulo, raízes complexas indicariam que as dimensões especificadas não são possíveis. Exemplo: A equação x² + x + 1 = 0 possui Δ = 1² -4(1)(1) = -3 < 0. As raízes são x = (-1 ± i√3)/2, que são números complexos. Se esta equação modelasse um problema físico, como a altura máxima de um projétil, a inexistência de raízes reais indicaria que a altura especificada não pode ser alcançada.
Em resumo, a resolução de equações do segundo grau, como demonstrado nos exercícios apresentados, envolve a compreensão de diferentes métodos e a capacidade de interpretar os resultados obtidos. A análise do discriminante permite prever a natureza das raízes, enquanto a verificação das soluções garante a precisão dos cálculos. A aplicação prática dessas equações em áreas como geometria, física e engenharia demonstra sua relevância e importância em diversas disciplinas.
Dominar esse conteúdo é crucial para o progresso em estudos matemáticos e científicos mais complexos.

