Exemplos De Numeros Racionais E Irracionais – Exemplos De Números Racionais E Irracionais: mergulhe nesse universo fascinante e desvende os mistérios que permeiam esses conjuntos numéricos. Você já se perguntou como diferenciar um número racional de um irracional? Quais são suas características e aplicações práticas? Prepare-se para uma jornada que explorará os conceitos, as propriedades e as aplicações desses números, desvendando suas nuances e revelando a beleza da matemática.
Ao longo deste estudo, você aprenderá a identificar, representar e utilizar números racionais e irracionais, compreendendo sua importância em diversos campos do conhecimento. Desvendaremos a natureza dos números racionais, que podem ser expressos como frações, e exploraremos a singularidade dos números irracionais, que desafiam a representação fracionária.
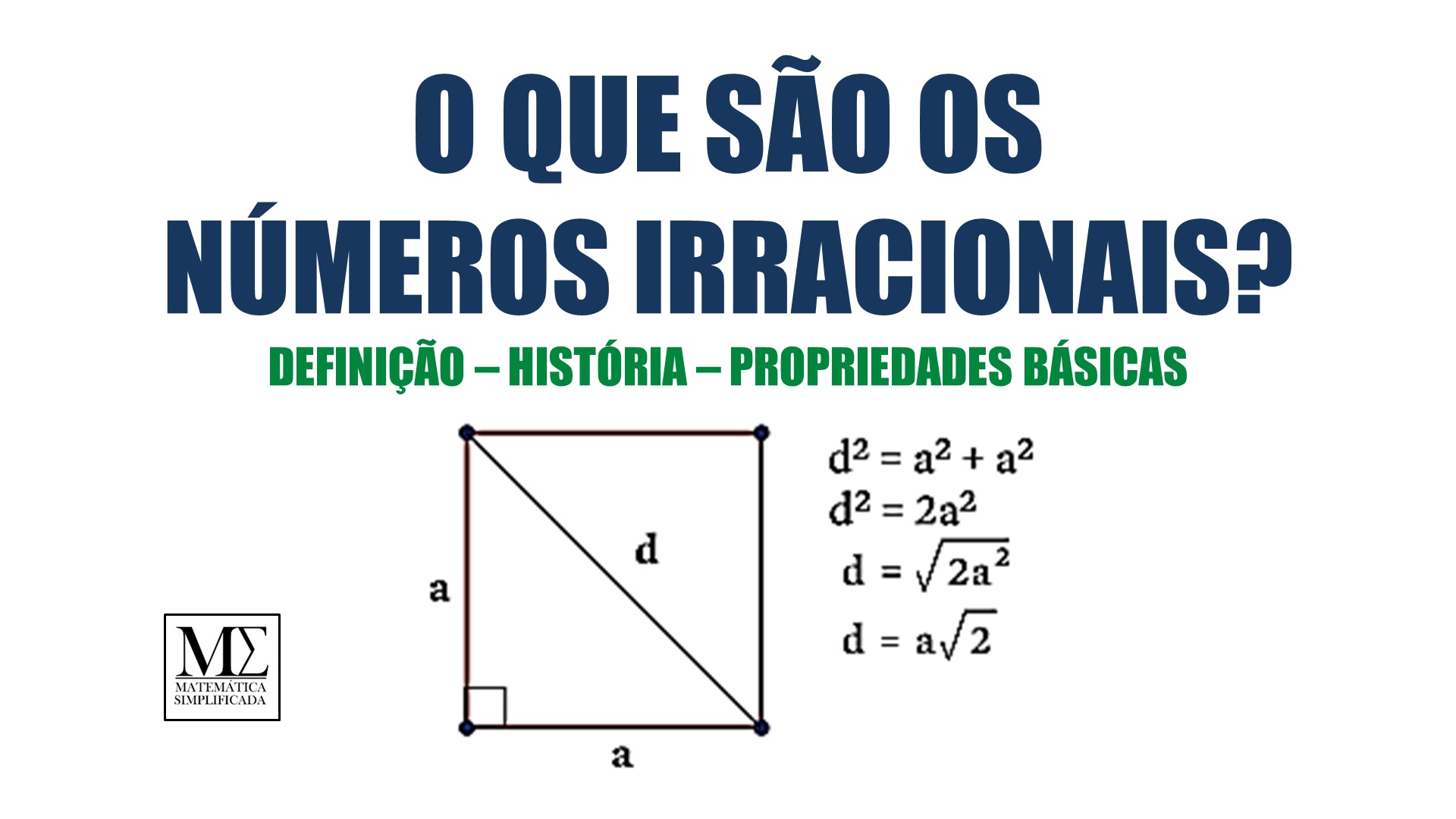
Abordaremos exemplos concretos, como o famoso número pi (π) e a raiz quadrada de 2 (√2), desmistificando a complexidade e revelando a beleza da matemática.
Introdução aos Números Racionais e Irracionais: Exemplos De Numeros Racionais E Irracionais
No vasto universo dos números, encontramos duas categorias principais: números racionais e números irracionais. Esses conjuntos numéricos possuem características distintas e desempenham papéis importantes em diversos campos da matemática, ciência e engenharia. Neste artigo, exploraremos a natureza desses números, suas representações, propriedades e aplicações.
Definindo Números Racionais e Irracionais
Números racionais são aqueles que podem ser expressos como uma fração, onde o numerador e o denominador são números inteiros e o denominador não é zero. Por exemplo, 1/2, 3/4 e -5/7 são números racionais. Em contraste, números irracionais não podem ser expressos como frações.
Eles possuem representações decimais infinitas e não periódicas. Exemplos de números irracionais incluem π (pi) e √2 (raiz quadrada de 2).
Propriedades Fundamentais
Os números racionais formam um conjunto denso, o que significa que entre quaisquer dois números racionais, sempre existe outro número racional. Eles também são fechados sob as operações de adição, subtração, multiplicação e divisão (exceto divisão por zero). Os números irracionais, por outro lado, não são densos e não são fechados sob essas operações.
Eles possuem propriedades únicas que os distinguem dos números racionais.
Representação de Números Racionais
Números racionais podem ser representados na forma de frações, como já mencionado. Por exemplo, o número 0,5 pode ser escrito como 1/2, e o número 1,25 pode ser escrito como 5/4. A representação decimal de um número racional é finita ou periódica.
Números decimais finitos, como 0,25, podem ser convertidos em frações dividindo o decimal pelo denominador apropriado (neste caso, 25/100, que pode ser simplificado para 1/4). Números decimais periódicos, como 0,333…, podem ser convertidos em frações usando uma técnica específica.
| Número Racional | Fração | Decimal |
|---|---|---|
| 1/2 | 1/2 | 0,5 |
| 3/4 | 3/4 | 0,75 |
| -5/7 | -5/7 | -0,714285… |
Representação de Números Irracionais
Números irracionais não podem ser expressos como frações. Eles possuem representações decimais infinitas e não periódicas. Isso significa que os dígitos após a vírgula decimal continuam infinitamente sem formar um padrão repetitivo. Exemplos de números irracionais conhecidos incluem π (pi), que representa a razão entre a circunferência de um círculo e seu diâmetro, e √2 (raiz quadrada de 2), que é a raiz quadrada positiva do número 2.
A representação decimal de π é 3,1415926535… e a representação decimal de √2 é 1,4142135623…
Diferenças entre Números Racionais e Irracionais
As principais diferenças entre números racionais e irracionais residem em suas representações, propriedades e aplicações.
| Característica | Números Racionais | Números Irracionais |
|---|---|---|
| Representação | Podem ser expressos como frações | Não podem ser expressos como frações |
| Decimal | Finito ou periódico | Infinito e não periódico |
| Densidade | Densos | Não densos |
| Fechamento | Fechados sob operações básicas | Não fechados sob operações básicas |
| Aplicações | Medidas, proporções, cálculos financeiros | Geometria, física, matemática |
Aplicações de Números Racionais e Irracionais
Números racionais e irracionais têm aplicações práticas em diversas áreas da vida.
Números racionais são usados em medidas, como comprimento, peso e volume. Eles também são essenciais em cálculos financeiros, como juros e taxas de câmbio.
Números irracionais desempenham um papel fundamental em áreas como geometria, onde π é usado para calcular a circunferência e a área de círculos. Em física, números irracionais são usados em cálculos relacionados a movimento, energia e ondas.
FAQ Summary
Qual a diferença fundamental entre números racionais e irracionais?
Números racionais podem ser expressos como frações, enquanto números irracionais não podem. Isso significa que os números racionais têm representação decimal finita ou periódica, enquanto os números irracionais têm representação decimal infinita e não periódica.
Quais são alguns exemplos de números irracionais na vida real?
O número pi (π), que representa a razão entre a circunferência de um círculo e seu diâmetro, é um exemplo clássico de número irracional. Outros exemplos incluem a raiz quadrada de 2 (√2) e o número de Euler (e).
Por que os números irracionais são importantes?
Os números irracionais desempenham um papel fundamental em áreas como geometria, física e matemática avançada. Eles são essenciais para a compreensão de conceitos como a irracionalidade do número pi, a natureza da raiz quadrada de 2 e a representação de grandezas contínuas.


