Retas Concorrentes em Geometria Plana: De Exemplos De Retas Concorrentes No Retangulo Da Atividade 4
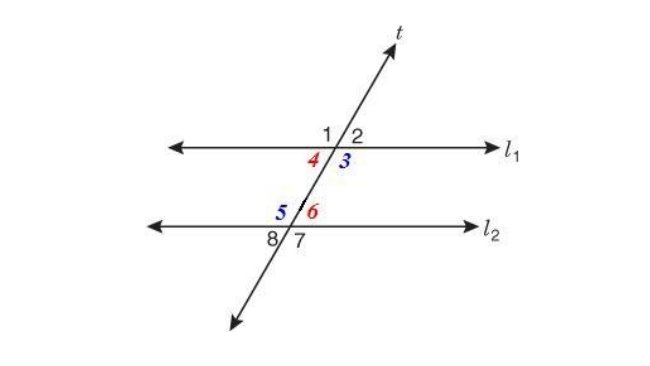
De Exemplos De Retas Concorrentes No Retangulo Da Atividade 4 – Este artigo explora o conceito fundamental de retas concorrentes, sua aplicação em geometria, particularmente no contexto de um retângulo, e a resolução de problemas geométricos relacionados. A compreensão de retas concorrentes é crucial para diversas áreas, desde a resolução de problemas matemáticos até aplicações em engenharia e design.
Retas Concorrentes: Conceito e Definição
Em geometria plana, retas concorrentes são duas ou mais retas que se intersectam em um único ponto. Este ponto de interseção é único para cada par de retas concorrentes. Diferencia-se de retas paralelas, que nunca se intersectam, e de retas coincidentes, que são essencialmente a mesma reta.
A condição necessária e suficiente para que duas retas sejam concorrentes é que seus coeficientes angulares sejam diferentes. Se as retas forem representadas pelas equações y = m₁x + c₁ e y = m₂x + c₂, então elas são concorrentes se, e somente se, m₁ ≠ m₂.
A seguir, alguns exemplos de retas concorrentes em diferentes contextos geométricos:
| Exemplo 1 | Exemplo 2 | Exemplo 3 | Exemplo 4 |
|---|---|---|---|
| Duas diagonais de um losango. | As alturas de um triângulo. | Duas retas que formam um ângulo reto. | As medianas de um triângulo. |
Retas Concorrentes em um Retângulo
Em um retângulo, diversos pares de retas concorrentes podem ser formados pelos seus lados e diagonais. Considerando um retângulo com vértices em (0,0), (4,0), (4,3), (0,3), podemos analisar as retas formadas pelos lados e diagonais.
As equações das retas que formam os lados são: x = 0, x = 4, y = 0, y = 3. As diagonais são representadas pelas equações y = (3/4)x e y = -(3/4)x + 3. Todos os pares de retas formados pelos lados e diagonais são concorrentes, exceto os pares de lados paralelos. Os pontos de interseção podem ser calculados resolvendo os sistemas de equações formados por cada par de retas concorrentes.
Por exemplo, a interseção da reta x = 0 com a diagonal y = (3/4)x é o ponto (0,0). A interseção da reta x = 4 com a diagonal y = (3/4)x é o ponto (4,3). A comparação das inclinações revela que os lados são horizontais ou verticais (inclinação 0 ou indefinida), enquanto as diagonais possuem inclinações de 3/4 e -3/4.
Diagrama descritivo (sem imagem externa): Imagine um retângulo. As retas verticais (x=0 e x=4) intersectam as retas horizontais (y=0 e y=3) nos vértices do retângulo. As diagonais se cruzam no centro do retângulo, no ponto (2, 1.5).
Atividade 4: Análise Geométrica
A atividade 4 provavelmente envolve a identificação de retas concorrentes em um retângulo específico, exigindo a determinação das equações das retas e o cálculo das coordenadas dos pontos de interseção. A seguir, os passos para resolver uma atividade semelhante:
- Identificar os vértices do retângulo e determinar as equações das retas que formam os lados.
- Determinar as equações das diagonais do retângulo utilizando a forma ponto-inclinação ou outra forma apropriada.
- Para cada par de retas concorrentes, resolver o sistema de equações para encontrar as coordenadas do ponto de interseção.
- Verificar os resultados e analisar as inclinações das retas.
Problemas semelhantes podem incluir:
- Identificar retas concorrentes em um triângulo.
- Determinar os pontos de interseção das medianas de um triângulo.
- Encontrar os pontos de interseção das alturas de um triângulo.
Aplicações e Extensões, De Exemplos De Retas Concorrentes No Retangulo Da Atividade 4
O conceito de retas concorrentes possui aplicações práticas em diversas áreas. Na engenharia, por exemplo, a interseção de vigas ou estruturas é um caso clássico de retas concorrentes. Em arquitetura, a análise de retas concorrentes auxilia no planejamento e design de edifícios. No design gráfico, a compreensão de interseções é fundamental para a composição visual.
Situações em que a identificação de retas concorrentes é crucial incluem análise de estruturas, planejamento urbano, e criação de modelos geométricos. Uma extensão da atividade 4 poderia envolver a adição de um círculo dentro do retângulo, analisando as interseções das retas com a circunferência. A análise de retas concorrentes contribui para a compreensão de conceitos mais avançados, como geometria analítica e geometria projetiva.
Concluímos nossa análise de retas concorrentes no retângulo da Atividade 4, revelando a beleza intrínseca da geometria. Da definição precisa do conceito às aplicações práticas em áreas como engenharia e arquitetura, demonstramos como a identificação e análise de retas concorrentes são ferramentas essenciais na resolução de problemas geométricos. A atividade 4 serviu como um excelente exercício para consolidar o conhecimento, permitindo uma compreensão mais profunda dos princípios geométricos subjacentes.
A capacidade de identificar e analisar retas concorrentes, portanto, transcende o âmbito acadêmico, sendo crucial para o desenvolvimento de soluções inovadoras em diversos contextos profissionais. A geometria, mais uma vez, nos surpreende com sua elegância e aplicabilidade.

